
Jeder hat mittlerweile schon die Begriffe Artificial Intelligence (AI) bzw. Künstliche Intelligenz (KI), Machine Learning (ML) und Deep Learning gehört oder gelesen. ChatGPT ist aktuell in aller Munde und auf Social Media will jeder zeigen, dass er auch schon mal mit ChatGPT “geredet” hat. Kurzum, das Thema erobert momentan die Welt und es wird nicht mehr lange dauern bis die Roboter die Weltherrschaft übernehmen. 🤖😉
Aber bevor es soweit ist, wollen wir uns heute anschauen, warum wir diese schönen Spielereien denn überhaupt machen können. Alles beginnt dabei mit einem Neuronalen Netz, welches sich aus vielen Neuronen zusammensetzt. Aber was genau ist denn jetzt so ein Neuron?
Im menschlichen Körper ist ein Neuron eine Zelle im Nervensystem, die Signale durch elektrische und chemische Prozesse überträgt. Dieses Neuron besteht aus einem Zellkörper, Dendriten und einem Axon. Dendriten empfangen Signale von anderen Neuronen, während das Axon Signale an andere Neuronen weiterleitet. Neuronen sind also als Grundbausteine des Nervensystems zu verstehen, welche uns das Denken, Fühlen und Handeln ermöglichen. 🧠
Im Bereich der künstlichen Intelligenz (kurz: KI) sind Neuronen die grundlegenden Elemente eines neuronalen Netzes. Dabei baut ein neuronales Netz auf der Idee des menschlichen Nervensystems auf. Ein künstliches Neuron im Rahmen eines neuronalen Netzes verhält sich ähnlich wie ein biologisches Neuron; es nimmt Input-Signale von Neuronen auf und gibt Output-Signale an andere Neuronen weiter. Der Unterschied ist, dass die Inputs und Outputs von künstlichen Neuronen numerisch sind und die Gewichte der Verbindungen zwischen ihnen von einem Algorithmus angepasst werden, um bestimmte Aufgaben zu lernen. Das hört sich jetzt erstmal sehr abstrakt an, richtig? Ich will daher versuchen, euch diese Abstraktion bildlich zu veranschaulichen.

Figure: Neuron mit drei Eingängen und einem Ausgang
In diesem Bild sehen wir, wie ein einfaches Neuron aufgebaut ist. Das Neuron hat mehrere Eingänge X1, X2 und X3 und einen Ausgang Y. Die Eingänge sind mit sogenannten Gewichtungen belegt; zu Eingang X1 gehört die Gewichtung W1, zu X2 gehört W2 und zu X3 logischerweise W3.
Das Neuron bildet nun aus den Eingängen und den Gewichtungen die Summe und gibt das Ergebnis an den Ausgang Y weiter, da wir von einer linearen Aktivierungsfunktion ausgehen. Was eine Aktivierungsfunktion ist, sehen wir weiter unten. Die Formel für die Berechnung sieht dabei folgendermassen aus:
|
|
Soweit so gut. Schauen wir uns nun an, wie wir mit einem Neuron eine Berechnung am Beispiel der linearen Regression anstellen können.
Neuron am Beispiel der linearen Regression
Wir wollen ein Neuron anschauen, welches mit Hilfe der linearen Regression eine Vorhersage macht. Man gibt hier Eingangswerte mit den dazugehörigen Resultaten vor und berechnet auf deren Basis dann die Vorhersage für einen beliebigen Eingangswert. Klingt kompliziert? Bringen wir also Licht ins Dunkle und schauen uns das ganze an einem simplen Beispiel an. Wir wollen Kilometer in Meilen umrechnen und haben folgende Informationen dazu:
10 km –> 6,21 Meilen
35 km –> 21,75 Meilen
85 km –> 52,82 Meilen
Bildlich würde dieses Neuron nun folgendermassen aussehen. Wir haben einen Eingang X1 mit einem Gewicht von W1 und einen Ausgang Y. Die Lineare Regression würde jetzt beispielsweise in unserem Neuron berechnet.

Figure: Neuron mit einem Eingang und einem Ausgang
Unser Neuron müsste nun also anhand der Formel für die lineare Regression die entsprechenden y Werte berechnen. Wer die Formel nicht parat hat, der kann hier einfach spicken:
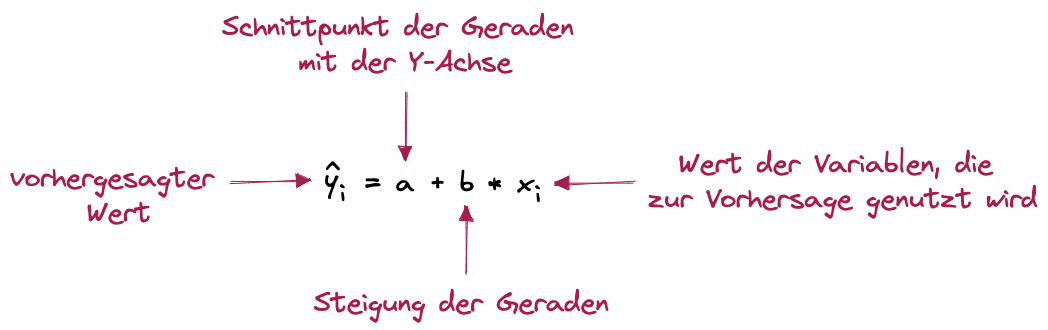
Figure: Regression – Statistik-Grundlagen
Nun, viele wissen jetzt wahrscheinlich nicht wirklich was damit anzufangen. Glücklicherweise gibt es hier Abhilfe. Python liefert uns beispielsweise ein Modul, mit dem wir einfach anhand der Werte, die wir zur Vorhersage verwenden, die lineare Regression berechnen können.
Hier ein solches Programm, welches diese Berechnung für uns durchführt:
|
|
Schauen wir uns den Code also mal genauer an. In Zeile 1 und 2 definieren wir die Punkte, welche uns als Ausgangslage für die Vorhersage dienen werden. Hier sei gesagt, dass es sich nicht wirklich um eine Vorhersage handelt, da es ja eine genaue Formel für die Umrechnung von Kilometern in Meilen gibt. Aber es dient uns als einfaches und anschauliches Beispiel. In Zeile 4 importieren wir vom Paket scikit-learn die LinearRegression-Funktion. Danach können wir uns in Zeile 5 ein neues model erzeugen. Dieses angelegte Modell trainieren wir in Zeile 6 mit den bereits bekannten Datensätzen. Nachdem das getan ist, können wir uns den Koeffizienten ausgeben lassen, also die Kennzahl, mit welcher wir von X nach Y kommen. Wir kriegen Y nun also durch die Berechnung von X = 250 * 0.62140936 = 155.35234.
Damit wir diese Berechnung nicht manuell durchführen müssen, bietet uns Python, bzw. scikit-learn eine Funktion, mit der wir die Vorhersage machen können. In Zeile 11 machen wir also basierend auf den berechneten Koeffizienten eine Vorhersage und erhalten die entsprechenden Werte.
Aktivierungsfunktion
Wir wissen nun also, wie ein einfaches Neuron funktioniert. Um zu verstehen, wie ein neuronales Netz funktioniert, fehlt uns aber noch ein entscheidender Baustein, nämlich die Aktivierungsfunktion. Eine Aktivierungsfunktion wird gebraucht, damit ein Neuron basierend auf seinen Eingängen aktiviert oder deaktiviert wird. Im obigen Beispiel haben wir gesehen, dass es einen linearen Zusammenhang zwischen dem Input und Output gibt. Neuronale Netze können aber mit linearen Abhängigkeiten nicht wirklich etwas anfangen. Warum das so ist, schauen wir uns schon sehr bald an. Was wir für ein neuronales Netz brauchen ist eine nicht lineare Abhängigkeit der bereitgestellten Parameter, um zu bestimmen ob ein bestimmtes Neuron aktiviert wird oder nicht. Wichtig an der Aktivierungsfunktion ist also, dass sie erstens aus einem linearen Wert einen nicht-linearen Wert machen kann und dass wir als Ergebnis einen Wert zwischen 0 und 1 bekommen. Weiterhin braucht es noch einen definierten Schwellenwert. Wenn der Output eines Neurons grösser ist als dieser Schwellenwert, so wird es aktiviert und das “Signal” an ein nachfolgendes Neuron weitergeleitet. Andernfalls bleibt es deaktiviert. Es gibt verschiedene Arten von Aktivierungsfunktionen, wie beispielsweise die Sigmoid-Funktion. Wie diese Funktion genau funktioniert, werden wir im Rahmen dieses TechUps aber nicht weiter anschauen.
Neuronale Netze
Nun wissen wir, wie ein einzelnes Neuron aufgebaut ist und wie eine Aktivierungsfunktion arbeitet. Gehen wir nun also einen Schritt weiter und schauen uns das Prinzip eines neuronalen Netzes genauer an. Neuronale Netze sind lernfähige Algorithmen, inspiriert von menschlichen oder auch tierischen Gehirnen, die mithilfe der bereits kennengelernten „Neuronen“ Eingangsdaten nach weitreichenden Schemata verarbeiten können. Neuronale Netzwerke bestehen dabei im Prinzip immer aus den folgenden vier Komponenten:
- Einem Input Layer
- Mindestens einem Hidden Layer
- Mindestens einer Aktivierungsfunktion
- Einem Output Layer
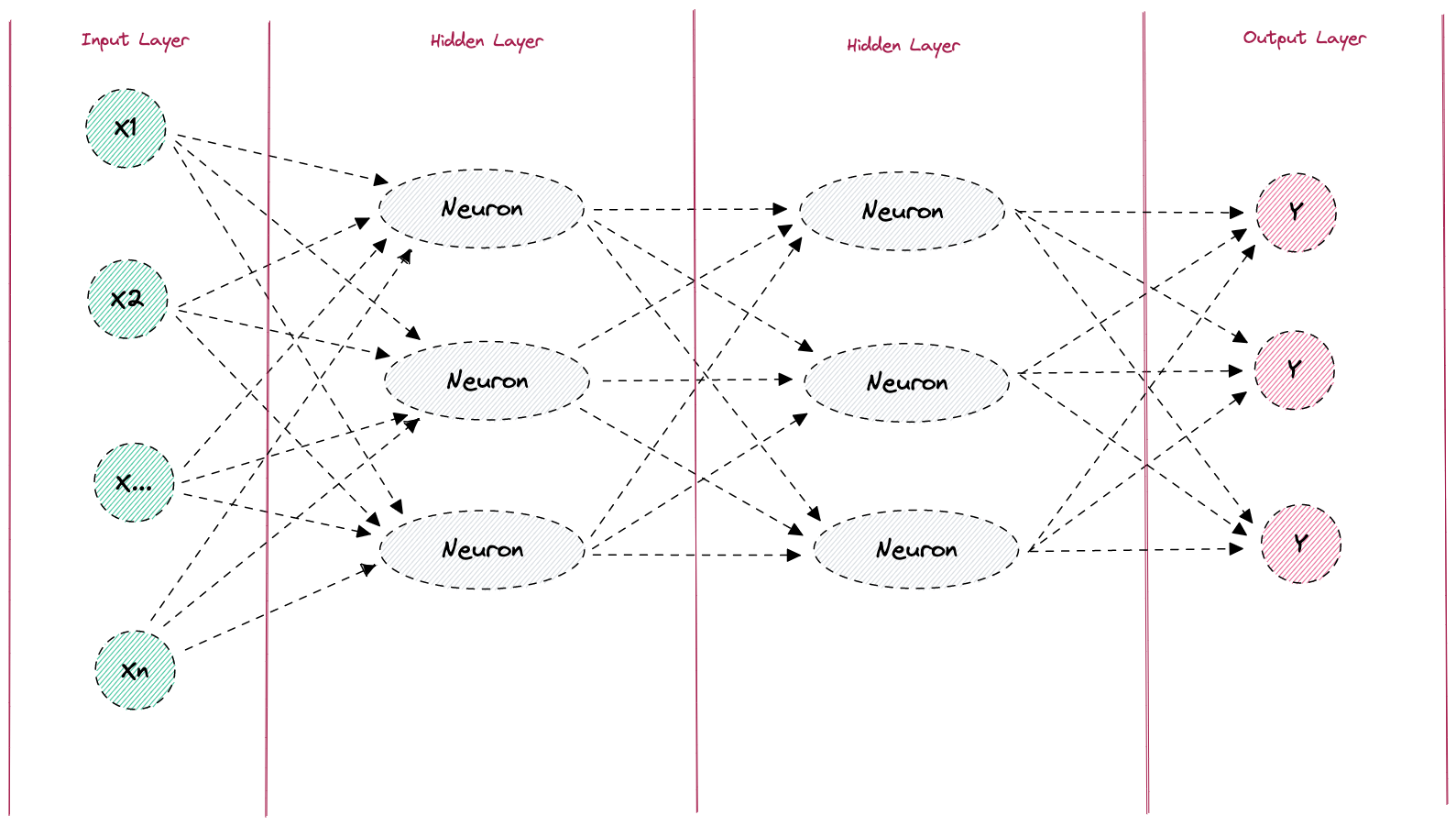
Figure: Neuronales Netz
Schauen wir uns doch am besten anhand eines praktischen Beispiels an, wie man nun mit so einem neuronalen Netz eine Vorhersage treffen kann. Ein praktisches Beispiel wäre hier zum Beispiel die Erkennung handschriftlicher Zahlen. Die Zahl, die wir erkennen wollen, geben wir als Input in unser neuronales Netz.
Im folgenden Bild sehen wir, wie eine Erkennung der Zahl 5 in einem neuronalen Netz möglich wäre.
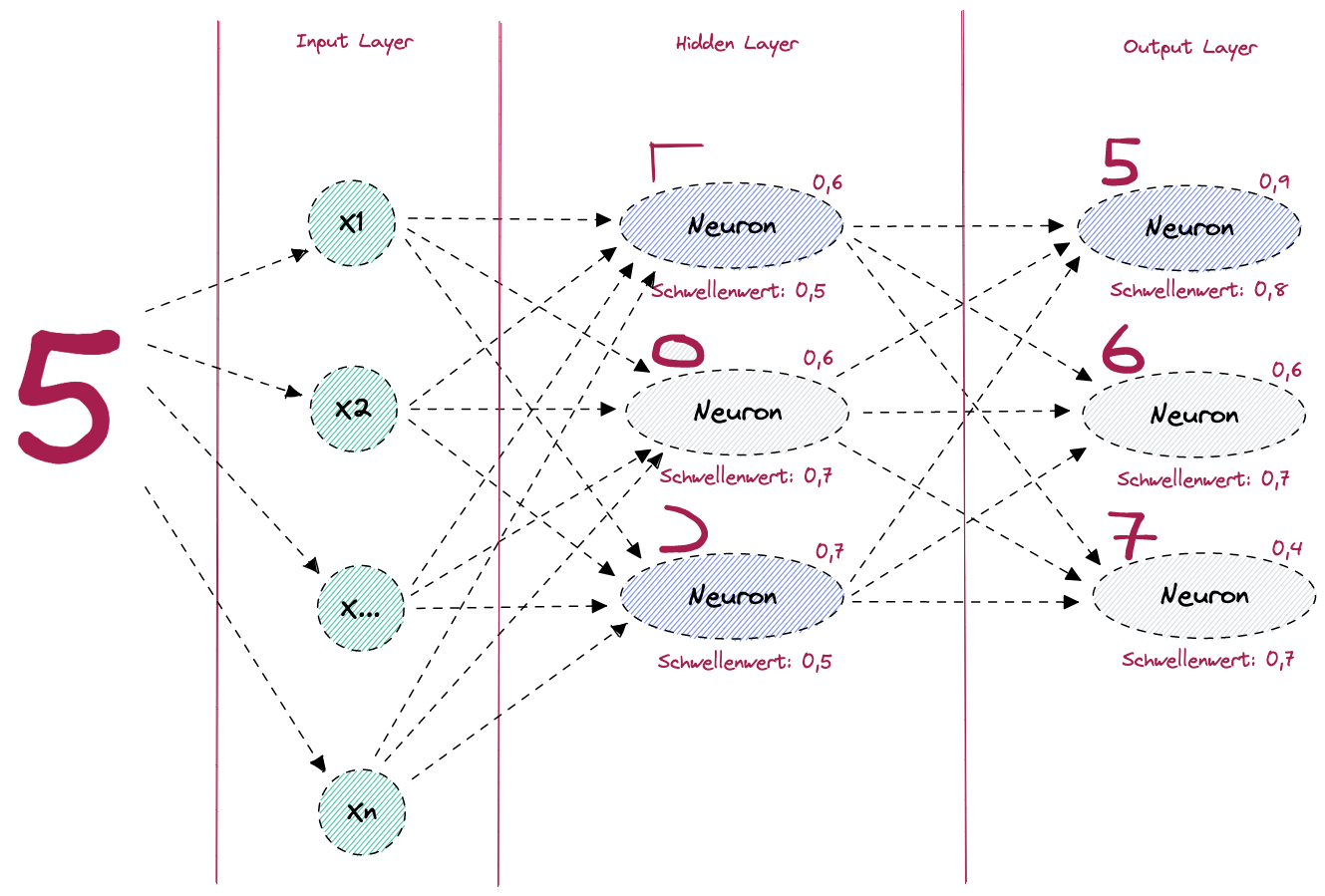
Figure: Neuronales Netz zur Erkennung der Ziffer 5
Im Bild sehen wir einen Input Layer, einen Hidden Layer und einen Output Layer. Jedes Neuron hat eine Aktivierungsfunktion, welche entscheidet, ob das jeweilige Neuron aktiviert wird (auch “feuert” genannt), oder ob es deaktiviert bleibt. Im Hidden Layer werden die beiden Neuronen aktiviert, welche den Formen entsprechen, aus denen die Zahl 5 gebildet wird. Das Neuron, welches den Kreis erkennt, bleibt in diesem Fall deaktiviert, weil der Schwellenwert von 0,7 nicht überschritten wurde. Im Output Layer wird dann das Neuron, welches die Zahl 5 erkennt mit dem Input aus Hidden Layer aktiviert und der Output an den Output Layer weitergegeben. Somit wurde von unserem neuronalen Netz vorausgesagt, dass es sich mit einer Wahrscheinlichkeit von 0,9 um die Zahl 5 handelt.
Was aber, wenn die Zahl nicht richtig erkannt worden wäre? In dem Fall müssten wir unser Modell trainieren.
Ein Modell trainieren
Jeder von uns hat das schon mal gehört. Wir müssen die künstliche Intelligenz trainieren, damit wir eine präzise Vorhersage bekommen. Was hat es aber mit diesem Training auf sich? Schauen wir uns dies anhand der Zahlenerkennung im obigen Beispiel genauer an.
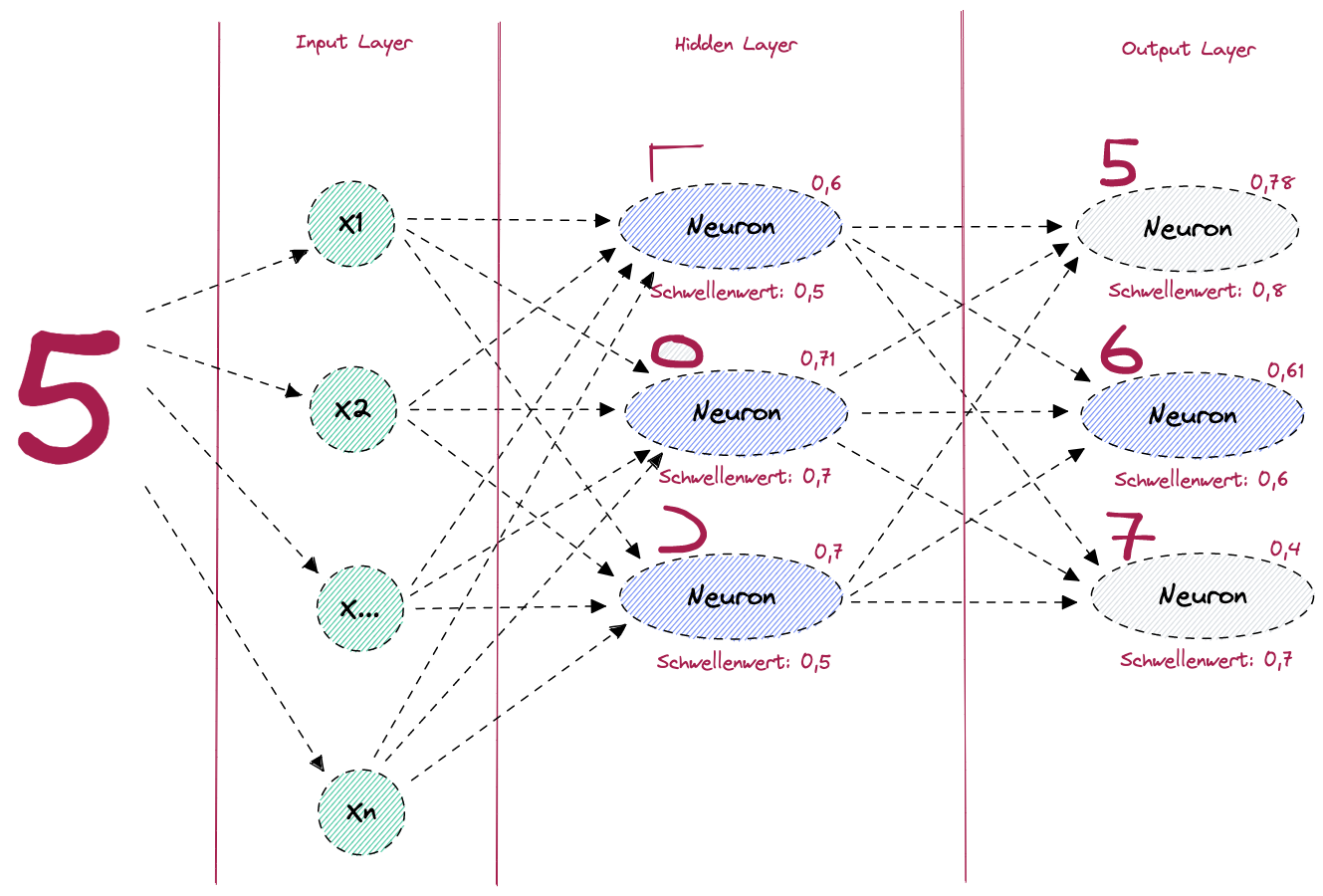
Figure: Neuronales Netz zur Erkennung der Ziffer 5 - Falsche Vorhersage
Im Bild sehen wir, dass versehentlich eine 6 erkannt wurde, statt der 5. Das ist passiert, weil der Schwellenwert des Neurons, welches die Zahl 6 erkennt, überschritten wurde und jener für die Erkennung der Zahl 5 nicht. Was müssen wir also tun, damit beim nächsten Mal das richtige Neuron aktiviert wird? Nun, der Schwellenwert des Neurons zur Erkennung der 5 muss überschritten werden und derjenige bei der 6 eben unterschritten. Kurz gesagt: Wir müssen einfach nur etwas an der Gewichtung bzw. am Schwellenwert “schrauben”. Der Fehler liegt hier offensichtlich beim Neuron im Hidden Layer, welches den Kreis erkennt. Dieses sollte nicht aktiviert werden, denn es verfälscht unser Resultat. Wie können wir aber nun die Gewichtungen und Schwellenwerte verändern, ohne darauf manuellen Einfluss zu nehmen? In einem neuronalen Netz erfolgt dies mittels der sogenannten Backpropagation (engl).
Backpropagation
Damit wir eine Backpropagation machen können, müssen wir erstmal den Begriff der Kostenfunktion (oder Verlustfunktion) einführen. In maschinellen Lernmodellen wird die Verlustfunktion bzw. die Kostenfunktion verwendet, um den Fehler zwischen den Vorhersagen eines Modells und den tatsächlichen Ausgaben zu messen. Je kleiner der Fehler ist, desto besser passt das Modell zu den Daten und desto höher ist seine Genauigkeit. Die Verlustfunktion bzw. die Kostenfunktion wird in der Regel bei der Optimierung des Modells verwendet, um die Gewichte und Schwellenwerte anzupassen und den Fehler zu minimieren. Das bedeutet, dass die Kostenfunktion essentiell ist, um unser Modell trainieren zu können.
Ein Beispiel für eine Kostenfunktion könnte dabei folgendermassen aussehen. Es sei hier gesagt, dass es noch weitere Kostenfunktionen gibt, welche wir aber im Rahmen dieses TechUps nicht betrachten werden.
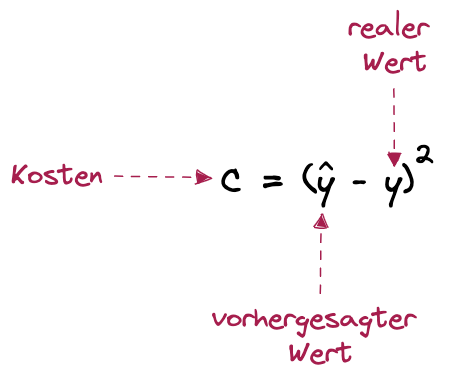
Figure: Neuronales Netz - Kostenfunktion Beispiel
Wir rechnen also einfach den vorhergesagten Wert minus den realen Wert, also den Wert, mit dem unser Model trainiert wurde. Je kleiner dieser Wert c ist, desto besser ist unser Modell trainiert. Aber wie können wir nun mit dem Feststellen der Kosten die Fehler minimieren. Nun brauchen wir wieder etwas Mathematik. Schauen wir uns das mal am Beispiel des einfachen Neurons von oben an:

Figure: Neuron mit einem Eingang und einem Ausgang
Solange wir unser Modell trainieren, ist der Wert Y (mit Dach) in diesem Bild der vorhergesagte Wert. Das heisst wir können die Gleichung folgendermassen auflösen:

Figure: Kostengleichung mathematisch auflösen - Schritt 1

Figure: Kostengleichung mathmatisch auflösen - Schritt 2
Da Y (ohne Dach) immer der reale Wert, also der Wert der aktuellen Berechnung ist und X1 immer ein fixer Input-Wert ist, sehen wir recht schnell, dass es in der obigen Gleichung nur einen Parameter gibt, an dem wir was verändern können, um die Kosten zu minimieren, nämlich W1; das Gewicht. Genau dies geschieht nun in der Backpropagation. Nach jedem Trainingslauf werden die Kosten berechnet und anschliessend die Gewichte mit dem Ziel der Minimierung dieser Kosten verändert. Das Bestreben ist hier, die Kosten möglichst nahe an den Nullpunkt zu bringen.
Mit dieser Erklärung schliesse ich mein heutiges TechUp und hoffe ich konnte euch die Grundlagen, bzw. das Grundverständnis, wie ein Neuron, und aufbauend darauf ein neuronales Netz funktioniert, näherbringen. Wir bei b-nova finden das Thema wirklich spannend und werden uns sicherlich weiter damit beschäftigen. Bleib dran! 🔥
Hier findest du ein weiteres tolles TechUp zu diesem Thema: Die Grundlagen von KI, Machine Learning und Deep Learning. 🚀